The Musical System of Archytas
Robert Erickson
The music theory upon which our conceptions of ancient Greek music are based starts with Aristoxenus who flourished around 318 B.C. Very little has been preserved of the earlier music theory relating to the music of the Classic period of Greece, the music praised, criticized and endlessly discussed in the works of such writers as Plato, Aristophanes and Aristotle. If more music had been preserved this would have been no great loss. In this absence our knowledge is based mostly upon opinions and observations which are often vague and conflicting about technical matters. The Orestes fragment and the mathematical formulations by Philolaus, Plato and Archytas are bits of solid evidence floating in a sea of opinion.
Archytas' ratios have been commented upon since antiquity (1) but their interrelationships have never been analyzed. I propose to show that Archytas' ratios present an interrelated intervallic system, and that the structure of the system offers valuable evidence about pre-Aristoxenian Greek music, especially about harmonia (2) and the technique of transposition, features which later were developed into complete systems of octave species and tonoi. (3)
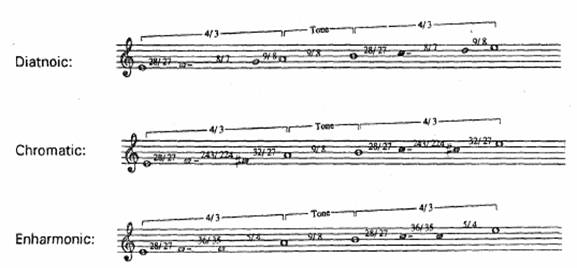
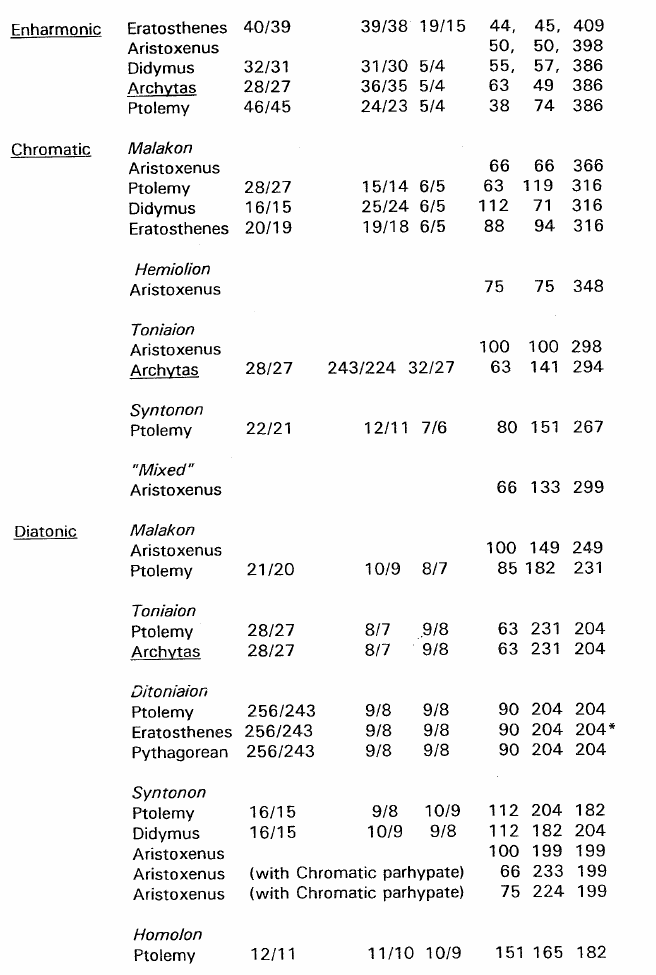
Archytas' ratios were preserved by Ptolemy (4), a set for each genus, as follows:
Enharmonic: 28/27 36/36 5/4
Diatonic: 28/27 8/7 9//8
Chromatic: 28/27 243/224 32/27
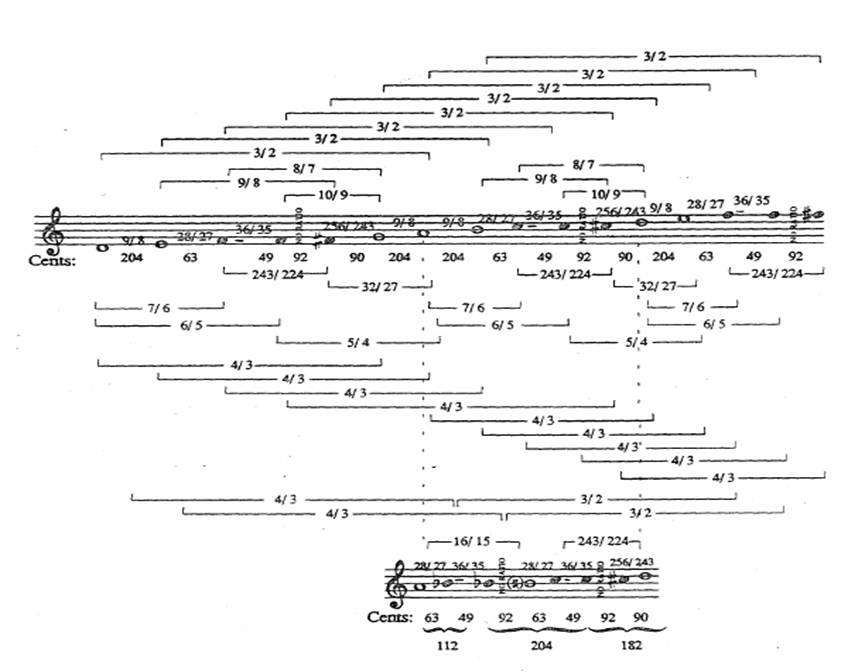
Each set represents the intervals of a tetrachord. If two tetrachords are separated by a tone, the conventional disjunctive, an octave scale can be constructed:
From A to c- in any of the above scales is the interval 7/6, (9/8 x 29/27 equals
7/6), a septimal minor third. (5) Therefore from F- down to an imagined lower D would be a 7/6
also. From A up to c in the enharmonic is a 6/5 minor third (9/8 x 28/27 equals 6/5)). Therefore from the imagined lower D up to F would be a 6/5 minor third too, and the fifths D
to A and A to e would be constituted: 6/5 x 5/4 equals 3/2. (6) Tannery first suggested
(7) that
Archytas ratios should be approached from this point of view, and that the fifth D to A is divided
by its harmonic mean F, the fourth A to d by its harmonic mean c-. Adopting Tannery's
suggestion we are able to set out the following framework in musical notation:

These calculations involving the harmonic mean place enharmonic lichanos (F) and trite (c-), and give an important clue to Archytas' other interval divisions too. Lichanos is the most sensitive tone in Greek tunings, for its placement determines the character of the largest interval in the tetrachord. The placement of trite is equally important to Archytas, for it creates both the 7/6 third and the pyknon interval 28//27, which appears in all three genera.
Significantly the division of the fourth and fifth is by the harmonic mean. (8) From Archytas' writings this might well be expected, for it was he who renamed the subcontrary mean harmonic because of its use in music, and he is responsible for the proof that no supraparticular ratio can be divided into equal rational parts. (9) If superparticular ratios cannot thus be divided it follows that for Archytas the most important method of division is the harmonic.
It appears that superparticular ratios were felt to produce "natural" musical
intervals throughout the whole development of Greek theory from Pythagoras to Ptolemy. This
conflict between Aristoxenus and the harmonists is really a quarrel between practicality and
analytical precision. (10)
When Pythagoras divided the octave he discovered the ratios for fourth and fifth; and these, 3/2 and 4/3, are superparticular. Hippasus and Philolaus show interest in superparticular ratios and the harmonic mean, and the attention paid to superparticular ratios and the harmonic mean, and the attention paid to superparticular ratios in the mathematical theory of irrationals has a background of practical music theory. (11) The interval system presented by Archytas' ratios harmonizes with his proof about the division of superparticular intervals, for all of his chief intervals are derived through the harmonic mean.
Therefore, we may be sure that the framework D to A to d was a fully conscious theoretical creation. It is the consequence of Archytas' desire to extend the scope of harmonic division.
The framework is blended with that of the usual two tetrachords separated by a disjunctive tone: E to A, tone, B to E. Together they make a structure either of two fifths, D to A to e, or tone/fourth,tone/fourth, D, E, to A, B to e. (See below.)

This framework, already containing the higher d, can be made into a double system by the addition of G: E to A, B to e is the same pattern as D to G, A to d, only a tone higher. These seven tones are the "standing" tones of Archytas' double system.

If diatonic and enharmonic are superimposed a new interval, the small second 10/9, is revealed:
 This important interval appears among the ratios (see Appendix B) of both
Didymus and Ptolemy. Its appearance in the enharmonic/diatonic mixture above is the first hint
that Archytas' ratios are somehow inter-related.
This important interval appears among the ratios (see Appendix B) of both
Didymus and Ptolemy. Its appearance in the enharmonic/diatonic mixture above is the first hint
that Archytas' ratios are somehow inter-related.
By combining diatonic and chromatic, it is possible to follow the development of Archytas' idea. Ptolemy (12) tells us that Archytas said that he placed chromatic lichanos (F#) in the relationship 256/243 to diatonic lichanos (G). Here is what happens when, following that hint, Archytas' diatonic and chromatic genera are combined. The first scale below shows the combination within the usual framework; the second gives a new scale running from F# to f#.
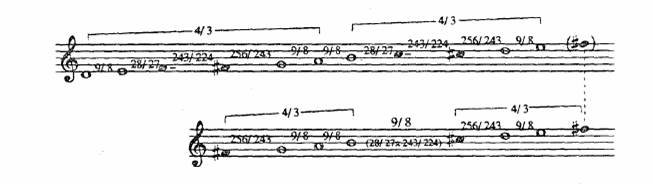
The scale which I have extracted in the Pythagorean scale, the most important and long-lived scale in music; (13) no doubt Archytas built his set of ratios in such a way as to make this tuning available, for his F# of the chromatic was by design calculated not from A but from G of the diatonic genus. Ptolemy disapproved but missed the point.
Clearly there is more to these ratios than the numbers for the three genera alone. Already we have found two varieties of diatonic; and there are more: in all, three diatonics, three chromatics and three enharmonics, all verified by later usage. In addition there are a number of tunings probably important to Archytas but not confirmed by others. The chart below superimposes all three sets of ratios for an overview of the main tunings available in the system. In order to accommodate the various scales, the range has been extended. Remarks beside each scale note identical or similar tunings by other composers. These tunings are all listed in Appendix B. For the tunings of Aristoxenus, who calculated in distances rather that ratios I have used the cents equivalents worked out by Winnington-Ingram in his "Aristoxenus and the Intervals of Greek Music". The pyknon, referred to below is the group of narrow intervals such as E to F- to F or, if uncleft, E to F or F# to G.
The system makes several other tetrachords available which, however, do not work out to be complete octave scales of two identical tetrachords. It is quite likely that they were intended by Archytas, and that they were used, for from what we know of practice, it was not unusual to mix tetrachords of various "shades" and genera. They all involve tetrachord synnemenon, using either B or B-. All are diatonic.

I have not included any ratios for the much discussed Spondeion scale; (14) but two
of Aristoxenus' chromatic "shades" are unaccounted for, and they may present two versions
or approximations of some of the intervals of the Spondeion:
Chromatic Malakon 66 66 366
Chromatic Meliolion 75 75 348
Now there is a tetrachord among Archytas' ratios with cents measurements as follows: 49, 92, 357. The 357 cent interval falls between the 366 and 348 of Aristoxenus with less than 10 cents difference either way. Archytas' 49 cents comes nowhere near 66 cents or 75 cents, but Archytas' 49 plus 92 equals the interval 141 cents, and this is within 9 cents of Aristoxenus' 75 plus 75 cents equal to 150 cents. Archytas' tetrachord splits the difference between Aristoxenus' Chromatic Malakon and Chromatic Hemiolion, and there is a fair presumption that all three tetrachords represent a single type. The tetrachord below, using B- instead of B for tetrachord synnemenon, may represent the Spondeion, with its special intervals, spondaismyus, sklysis and ekbole, as mentioned by Aristides and Bacchuis. Winnington-Ingram points out that Bacchius illustrated these intervals using the same part of the scale we are considering, at the point of conjunction or disjunction of the tetrachords. (15)

Ekbole: 5 dieses Spondaismus: 3 dieses Eklysis: 3 dieses In Aristoxenian terminology a diesis equals a "quarter-tone".
Three-quarters of a tone equals about 148 cents.
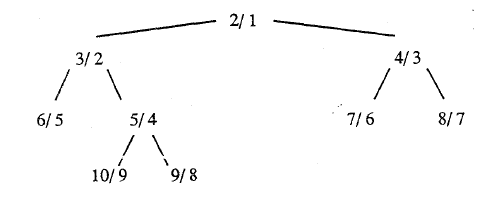
All of the main intervals in the Archytas system are derived through the harmonic mean. The large intervals are derived as follows (16):
The small intervals are also a result of manipulation of the harmonic mean:
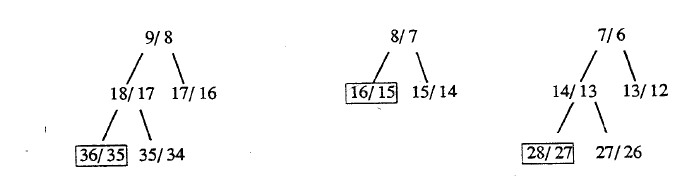
The interval 243/224 is not superparticlar, and probably Archytas regarded it as a limma (literally "the rest") in the same way that 256/243 is a limma. Ptolemy criticized Archytas severely for this "ekmelic"interval (17) on the grounds that Archytas is measuring from genus to genus to make it and that it is no ratio. The interesting point, however, is that Archytas manages to divide that interval 243/224 into two parts, 49 cents and 92 cents. I believe the 92 cents part is the most significant, because it is auditorialy identical to 90 cents, the Pythagorean limma of 256/243. In effect Archytas makes it possible to begin tetrachords from either F or F# with a well known and traditional interval. This fact alone points toward a system. Coupled with the documentation by the tunings of other composers, especially Aristoxenus, I think we can be certain that Archytas' ratios were constructed in such a way that they made and were meant to make an interrelated tuning system.
Archytas' System and the Harmoniai from Plato's Republic
The famous discussion from Book III of the Republic includes mention of a number of harmoniai: Dorian, Phyrgian, Lydian, Mixolydian and Iastian. Music in these harmoniai is supposed to have strong psycho-physical effects. These effects, their, nature and power, have been the subject of speculation ever since antiquity. With the help of Archytas' system it is possible to reconstruct the actual sounds of the fourth century harmoniai. Fitting the harmoniai to the system will give us not only an excellent auditory impression of the sounds Plato heard - that would be worth something in itself - but show some of the reasons why Archytas might have invented his system.
Plato's harmoniai were preserved by Aristides Quintilianus (18), as recipes (Dorian: tone, diesis, diesis, diton, tone diesis, diesis, ditone) and in letter notation. They are different from the octave scales of later Greek theory. Dorian and Phrygian have a range of a ninth (compare Archytas' framework), others less than an octave. Some omit one or more tones, and Iastian and Mixolydian have diatonic elements, even though the prevailing genus is enharmonic.
Several of the harmoniai are said to be "malakon", an epithet later applied to "soft" tetrachords, such as those containing 8/7 and 7/6 tones rather than 9/8 tones. (19) One of the Lydians is called Syntonolydian, usually taken to mean high in pitch, or intense, or both. Another of the Lydians is called "chalaros" - "low and lax", or "slack". From these terms it appears that harmoniai may begin at various degrees of a tuning system. It may be only a coincidence that Plato's Dorian and Phyrgian together require a range of a ninth, and that the tuning system of his friend and colleague, Archytas, has a ninth for its framework. Could both have been following some sort of current practice? Such as the Iasti-Aioli tuning described below?
At any rate it appears that Archytas has created a system in which a number of harmoniai can be played, at various degrees and in various shadings, and which permitted easy modulation by pitch degree and/or genus and "shade." Since Archytas' system and Plato's harmoniai are contemporary it seems reasonable to take them together to construct a model of fourth century harmoniai in a fourth century tuning system. (20)
First the Iastian (Ionian), by way of example. Aristides recipe is dieses, diesis, diton, a three semitone interval (trihemitone) and a tone. He points out that "this scale was a tone less than the octave". His terms are Aristoxenian: a diesis is a quarter of a whole tone; a ditone, two whole tones; trihemitone, a tone and a half. Practically, the ditone is a "large third", either the Pythagorean major third or the 5/4 third. The trihemitone is any sort of minor third, narrow or wide. A diesis may vary from about 45 cents to something rather large. The dieses from Archytas' system are 28/27 and 36/35. The dieses make up the pyknon.
The Iastian harmonia has a tetrachordal structure of two conjunct fourths. All of the variants in the example below preserve that structure, though the interior intervallic relationships may change with transposition. A certain "shade" of the Iastian is mentioned, malakon, and this variety of Iastian is especially identified with drinking parties and soft living. Plato considered it unfit for the ears of his warrior-trainees.

I have included one each of diatonic and enharmonic forms of the Iastian for comparison. The
reader may wonder which of the four enharmonics is the "right" tuning. My feeling is that all
of those shown, and probably such others as could be gotten from the system would have been
used, either for convenience or by design. The intonations change but the fundamental
structure is identifiable. The Iastian enharmonic #4 is my candidate for the sort of malakon
Plato was against, with its up to date 5/4 third and thoroughly unpythagorean upper tetrachord; its uncleft pyknon leans it toward the diatonic.
Other Iastians are available in the system; I hope I have shown enough to indicate the scope of possible modulation. The significant point is that modulation by pitch degree often is accompanied by a shading of genus. The two types of modulation go together.
All of Plato's harmoniai fit into Archytas' system on at least two scale degrees, some of them with a number of changes of genus and "shade." There are many more modulatory possibilities than I have shown below, with only two positions for each of the remaining harmoniai. From the internal structure of any harmonia the reader can easily work out which system degrees it can transpose to.
 Aristides gives the Dorian in this form. Later it runs from E to e.
Aristides gives the Dorian in this form. Later it runs from E to e.

"High and "dirge-like". This lower tetrachord is chromatic. Compare below.

The fact that the harmoniai can begin on various scale degrees brings up the question: are they primitive octave species? I think not, even though some significant correspondences appear. The seven octave species (see note #3) compare well with the harmoniai except for the beginning note of the Dorian.

These pitch correspondences are striking, but should not be taken as proof that harmoniai were octave species. When theorists such as Aristoxenus set out to systematize scale theory it is possible either that the old harmoniai had been torn to tatters by modulation and chromaticism or that the intervallic relationships proper to any harmonia were a matter of melodic tradition.
There is less direct relationship between the harmoniai and the later tonoi, but the concept of tones carries a connotation of a (theoretically) transposed system, and we can view Archytas' system as a congeries of systems beginning on B, C-, D, E, F-, F, F# etc., and integrated into a single whole. More than anything else this whole resembles one of those "close-packed" diagrams discussed by Aristoxenus. Unfortunately, everything we know about these "close-packed" diagrams comes from him, but what he says is tantalizing:
And in dealing with the affinity between scales and regions of the voice we must not follow the Harmonists in their endeavor at compression, but aim rather at the intermodulation of scales, but considering in what keys the various scales must be set so as to admit of intermodulation. We have shown in a previous work that, though as a matter of fact some of the Harmonists have touched on this branch of our subject in a purely accidental way, in connection with their endeavour to exhibit a close-packed scheme of scales, yet there has been no general treatment of it by a single writer belonging to this school. This position of our subject may broadly be described as the part of the science of modulation concerned with melody. (21)
Certain characteristics of Archytas' system harmonize with the theory of high and low tuning elucidated by Otto Gombesi (22): fairly large number of harmoniai can begin on either E or F-. However, there are several other "good" degrees, D, E, F-, and F#. The structure of the system is especially designed for Pythagorean shadings from F#.
All in all the evidence shows that the harmoniai were neither embryonic octave species nor tonoi, even though certain characteristics of their behavior in what appears to be a "close-packed" system may have been significant for later developments.
To get back to firmer ground, we can say that we have here a modulating system adapted to the fourth century harmoniai. This is implicit in the framework itself (refer back to page 89 - 90.) The fixed notes indicate a two mese system, but since beginnings may be made from a number of pitch degrees it is really a multiple-mese system. It allows any harmonia to be modulated by pitch degree, and, as shown above, the change of pitch degree may be accompanied by a change of "shade" or genus, depending upon the harmonia and the degree chosen.
Much more art was involved that simple transposition by a fourth up or down. A rich modulatory technique must be assumed, and this is strongly supported by the contemporary literary evidence, where there are copious references to modulation and mixing of the genera. Plato's criticisms of the kitharists who mix all the harmoniai together and create a chromatic confusion are all the more instructive for being negative. (23) The patterns of such elaboration are built into Archytas' system, and it looks very much as though it were designed to accommodate the practice of those very musicians whose performances were so distasteful to Plato.
Archytas' system resembles a number of the tunings used by those kitharists, and it corresponds most closely to Iasti-Aeoli, at the most favored system.

The range of a ninth invites the thought that Archytas had in mind just such a tuning convention when he designed his ratios. By the time of Ptolemy the enharmonic had fallen out of fashion, and that is why Iasti-Aioli is oriented toward chromatic/diatonic. From Aristoxenus we know that the enharmonic was old-fashioned when he was writing his Harmonics, and the fourth century literary evidence shows chromatic and diatonic as the "new sound" during Archytas' lifetime too.
The significant parallels between Iasti-Aioli and Archytas - range, identity of tetrachords, modulating system are strong enough so that at the very least we may be sure that Archytas' ratios are numerical shorthand for a modulating tuning system. In both systems tetrachord relationships are ordered in such a way that a diatonic/chromatic tuning mix is procured. Archytas' system provides additionally a complete tuning basis for selected pairs of (sometimes different) tetrachords. Presumably players always tuned for genus color, modulatory possibilities and convenience. In Archytas' time these patterns provided the materials from which various harmoniai were constructed. Harmoniai could be played from various pitch degrees and with certain modifications of "hardness" and "softness". The amount and variety of modulation presumably depended upon the number of pitches available on an instrument. Apparently much was possible on a nine-string lyre tuned in Iasti-Aioli. It is not unthinkable that, given the notorious conservatism of instrumental practice and technique, Ptolemy's Iasti-Aioli represents a tuning practice hundreds of years old, and that it existed in this form during Archytas lifetime.
From what has been said it is clear that I do not regard Archytas' system as a paper abstraction. That means that it would have to be tuned by an ordinary musician rather than a scientist. I believe it was fairly easy to tune, on say a lyre or a harp, only slightly harder than Pythagorean.
Pythagorean is tuned by fifths and fourths, what the Greeks called "tuning by consonance". (25) For example, if one wished to tune the diatonic, E,F, G,A,B,C,D,E, one proceeded this way:


This would produce the Pythagorean diatonic with limmas of 256/243 for half-steps, provided the player had tuned well. F# and G# could be added in the same manner:
(B) c#
F# (F#)
It is likely that the tuning error was plus or minus more than four cents, since even on a monochord the error cannot be reduced further than that. (26)
Archytas' diatonic could be tuned as follows :

The player sets only one interval by ear, D to F-. Even so, he is able to use an emmelic interval - he never tunes a pyknon interval directly. From a practical point of view this is a most important consideration, for no man is going to be able to tune say a 19/18 interval. Humans are very good at octaves, fifths and fourth, able to tune a third in a triad to get rid of beats, but otherwise quite insensitive to the ratios of small intervals having large fraction ratios.
To complete the system the player tunes to complete a Pythagorean diatonic scale: F#,G,A,B,c#,d,e,f#. Since G,A,B,d and e are already tuned he needs only to tune F# and c#.
The best thing about this analysis of Archytas' ratios is that it has given us a way to reconstruct with certainty the actual sound of fourth century Greek music. With a little practice one ought to be able to compose other sources of Greek music, and this would be a valuable way to explore the possibilities of the system and its musical characteristics. The system in turn, might well help solve some problems of detail in the transcription and reconstruction of the antique musical fragments.
In summary we find that an analysis of Archytas' ratios reveals:
1. A tuning system which structures modulation
(a) by pitch
(b) by genus or "shade"
2. Which reflects practical music making
(a) it is easy to tune
(b) it makes available all the important intervals of
Greek music
3. Which includes many of the tunings duplicated by later theorists.
(a) Aristoxenus: 4
(b) Erastosthanes: 2
(c) Didymus: 1
(d) Ptolemy: 3
(e) Aristides Quintillianus: Spondeion.
4. Which provides, with Plato's harmoniai, a theoretical model of the
structure of fourth century Greek Music.
Practical, elegant in design, it is worthy of the ingenuity of the man who
generalled a city, built a wooden dove that would fly, wrote musical and political theory and
solved one of the great mathematical problems of antiquity, the duplication of the cube. This
new knowledge gleaned from his ratios can be used to illuminate several dark places in the
history of fourth century Greek music and music theory. Linked to other studies our whole view
of ancient Greek music might be considerably widened.
(San Francisco: February/March/April 1965)
Appendix A - Intervals with their Equivalents in Cents
2/1 1200 7/6 267 13/12 139
3/2 702 8/7 231 16/15 112
4/3 498 9/8 204 19/18 94
81/64 408 10/9 182 256/243 90
5/4 386 11/10 165 20/19 89
6/5 316 12/11 151 28/27 63
32/27 294 243/224 141 36/35 49
Appendix B - Tuning Ratios From Antiquity
Appendix C:
1. Ptolemaios und Prophyrios uber die Musik, Ingemar During, Goteborg, 1942, especially Chapters 13 and 14. Aristoxenus, Harmonics, ed. H.S. Macran, Oxford, 1902, 52 ff. Aristoxenus and the Intervals of Greek Music, R.P. Winnington-Ingram, C.Q. 26, 1932, pp. 203, 205, 206. The Musical Scales of Plato's Republic, J.F. Mountford, C.Q. 17, 1923. "The Harmonics of Ptolemy," J.F. Mountford, Transactions of the American Philological Association, LVII, 1926, p.81. Harmonielehre der Pythagorer, B.L. van der Waerden, Hermes 78, 1943, p.185.
2. A harmonia is fundamentally a tuning (Grove Dictionary) the word may include the meaning of "scale". A definition which is true to its meaning through Plato, and the sense in which the term will be used in this paper is: an ordered array of tones. See also Musical Thought in Ancient Greece, Edward A. Lippman, New York, 1964, Ch.I.
3. To Aristoxenus and Ptolemy octave species were octave segments cut successively from a two octave diatonic system; but species could also be chromatic or enharmonic. See Grove Dictionary p.775. The seven species of diatonic octaves are:
B c d e f g a b Mixolydian
c d e f g a b c1 Lydian
d e f g a b c1 d1 Phrygian
e f g a b c1 d1 e1 Dorian
f g a b c1 d1 e1 Hypolydian
g a b c1 d1 e1 f1 g1 Hypophrygian
a b c1 d1 e1 f1 g1 a1 Hypodorian
Tonoi and octave species are related. A tonos has the name of that species (of the octave) whose characteristic series of intervals it brings within a central range of pitch, for example the central octave of the Dorian tonos. It is reasonable to assume that the original purpose of the tonoi was to bring the species within this range, and that the species received their names, not as segments of the Great Perfect System, but as different series of intervals within the same range." Grove, p.776. Tonoi are sometimes called "transposition scales" in older literature, but Gombosi, "Key, Mode, Species", JASM, 4, 1951, has argued that
4. Ptolemaios und Prophyrios uber die Musik, p.47. Ptolemy is our source for most of the ratios of antiquity. All of the ratios mentioned in this paper are given below in Appendix B.
5. This interval is our "blue third", head in Jazz and folk music. For a discussion of its use and characteristics see Report on Organization in Auditory Perception, P.C. Boomsliter and Warren Creel, Albany, NY., 1962, and recorded examples accompanying the booklet.
6. Intervals are added together by multiplying their ratios. For convenience to the reader all the intervals mentioned in this paper and their equivalents in cents are listed in appendix A.
7. Memoires Scientifiques, III, M.P. Tannery, p.247.
8. Archytas' definition of the harmonic mean, Ancilla, Freeman, Oxford 1962: "by whatever part of itself the first term exceeds the second, the middle term exceeds the third by the same part of the third. In this proportion the ratio of the larger numbers is larger, and of the lower numbers less." e.g., 6,4,3; 6-4=2, 4-3=1, and 2:6=1:3; 6/4 is greater than 4/3.
9. Preserved by Boethius, Diels-Kranz A19.
10. Aristoxenus was the exception. His criticism of all his predecessors is based upon the conception of a "good enough" interval, and he was aware that more than proper tuning was involved in music. His recipes show that he accepted the same musical intervals - give or take a few cents - which are stated as ratios by others. See appendix B.
11. Companion to the Pre-Socratic Philosophers, K. Freeman, Oxford, 1959: Hippasus, p.86, Philolaus, p.224. For relations between theory of irrationals see "Theaetetus and the Theory of Numbers," A. Wasserstein, C.Q. 52, 1958, 172 ff.
12. Ptolemaios und Porphyrios über die Musik, p.47.
13. Until now the earliest complete statement of its ratios was thought to be by Plato in his Timaeus, and a few scholars have even argued that the scale was invented by Plato himself.
14. Musical Scales of Plato's Republic, J.F. Mountford. "The Spondaeion Scale," R.P. Winnington-Ingram, C.Q. 22, 1928.
15. "Aristoxenus and the Intervals of Greek Music," p.205.
16. Significantly there are ten intervals, using numbers up to ten, an elaboration of the original Tetraktys of the Decad.
17. Ptolemaios und Porhpyrios uber die Musik p.48.
18. Aristides Quintillianus, De Musica ed. R.P. Winnington-Ingram, Teubner texts, 1963. "Aristides Quintillianus," Von der Musik, Rudolph Schafke, Berlin, 1937, pp.192-3.
19. Plato's Republic p.399. The Rise of Music in the Ancient World. C. Sachs, New York: 1943, p.212, 228. Studies in Musical Terminology in Fifth Century Literature, Ingemar During, Eranos 43, 1945, p.180.
20. J.F. Mountford first applied Archytas' basic set of ratios to Plato's harmoniai. See his Musical scales of Plato's harmoniai. See his "Musical Scales of Plato's Republic".
21. Harmonics, p.170.
22. "New Light on Ancient Greek Music," O.Gombosi, Papers of the International Congress of Musicology, New York, 1939. Tonarten und Stimmungen der Antiken Musik, Copenhagen, 1939, Otto Gomvosi.
23. Laws, 669; Republic, 397. See also During in Studies in Musical Terminology, for his translation of the Pherecrates fragment quoted in Pseudo-Plutarch. The attitudes expressed are those of the musically conservative party to which Plato belonged, and During dates the fragments to 410 B.C., at which time Plato was about 18 years old. He grew up hearing - and resisting - the new chromatic/diatonic practice.
24. Ptolemaios und Porphyrios uber die Musik, pp. 200-215, especially p.208.
26. The best error on a monochord with a one meter string is about 4 cents, according to C.D. Adkins, Theory and Practice of the Monochord, University Microfilm 64-3344, Ann Arbor. For tuning ability by professional factory "fine tuners" who can tune within 2 cents only with a visual device, and then only in the middle octave of the piano, see JASA Vol.33 #5, p.582. In the experience of musicians, 2 cents is a distinguishable lower limit in the case of fourths, fifths and octaves. Other intervals, major and minor thirds, sixths, remain acceptable, if the musical situation permits, within a large cents range. Whole and half-tones may vary widely, again depending upon the musical situation. Many of the intervals discussed in this paper may be heard in our present day concert and popular music; the interval 7/6 is the "blue third"; 10/9 intervals are quite common, 8/7 somewhat rarer, but the Pythagorean third is as "natural" as our equal temperament third; as to small intervals, our non-keyboard players use all sizes, the 256/243 and 16/15 approximations being the most usual. Anyone may verify this for himself: tune some of the intervals you wish to study, or have them tuned by professional tuner. Then listen carefully to the actual intervals sung or played by musicians. Check back to the pre-tuned sounds.